Once you take a look at your surrounding surroundings, it would seem to be you’re residing on a flat airplane. In any case, this is the reason you may navigate a brand new metropolis utilizing a map: a flat piece of paper that represents all of the locations round you. That is seemingly why some folks previously believed the earth to be flat. However most individuals now know that’s removed from the reality.
You reside on the floor of an enormous sphere, like a seaside ball the dimensions of the Earth with a couple of bumps added. The floor of the sphere and the airplane are two attainable 2D areas, that means you may stroll in two instructions: north and south or east and west.
What different attainable areas may you be residing on? That’s, what different areas round you might be 2D? For instance, the floor of an enormous doughnut is one other 2D house.
By a area referred to as geometric topology, mathematicians like me research all attainable areas in all dimensions. Whether or not attempting to design safe sensor networks, mine knowledge or use origami to deploy satellites, the underlying language and concepts are prone to be that of topology.
The form of the universe
Once you look across the universe you reside in, it seems to be like a 3D house, identical to the floor of the Earth seems to be like a 2D house. Nevertheless, identical to the Earth, in the event you have been to have a look at the universe as an entire, it could possibly be a extra difficult house, like an enormous 3D model of the 2D seaside ball floor or one thing much more unique than that.
A doughnut, additionally referred to as a torus, is a form which you can transfer throughout in two instructions, identical to the floor of the Earth.
YassineMrabet through Wikimedia Commons, CC BY-NC-SA
When you don’t want topology to find out that you’re residing on one thing like an enormous seaside ball, realizing all of the attainable 2D areas will be helpful. Over a century in the past, mathematicians discovered all of the attainable 2D areas and plenty of of their properties.
Previously a number of a long time, mathematicians have discovered rather a lot about all the attainable 3D areas. Whereas we shouldn’t have a whole understanding like we do for 2D areas, we do know rather a lot. With this information, physicists and astronomers can attempt to decide what 3D house folks really stay in.
Whereas the reply is just not fully identified, there are a lot of intriguing and stunning prospects. The choices change into much more difficult in the event you contemplate time as a dimension.
To see how this may work, notice that to explain the situation of one thing in house – say a comet – you want 4 numbers: three to explain its place and one to explain the time it’s in that place. These 4 numbers are what make up a 4D house.
Now, you may contemplate what 4D areas are attainable and during which of these areas do you reside.
Topology in increased dimensions
At this level, it might seem to be there isn’t a motive to think about areas which have dimensions bigger than 4, since that’s the highest possible dimension that may describe our universe. However a department of physics referred to as string idea means that the universe has many extra dimensions than 4.
There are additionally sensible functions of enthusiastic about increased dimensional areas, similar to robotic movement planning. Suppose you are attempting to know the movement of three robots transferring round a manufacturing facility ground in a warehouse. You may put a grid on the ground and describe the place of every robotic by their x and y coordinates on the grid. Since every of the three robots requires two coordinates, you have to six numbers to explain all the attainable positions of the robots. You may interpret the attainable positions of the robots as a 6D house.
Because the variety of robots will increase, the dimension of the house will increase. Factoring in different helpful info, such because the areas of obstacles, makes the house much more difficult. As a way to research this downside, it’s worthwhile to research high-dimensional areas.
There are numerous different scientific issues the place high-dimensional areas seem, from modeling the movement of planets and spacecraft to attempting to know the “shape” of huge datasets.
Tied up in knots
One other kind of downside topologists research is how one house can sit inside one other.
For instance, in the event you maintain a knotted loop of string, then now we have a 1D house (the loop of string) inside a 3D house (your room). Such loops are referred to as mathematical knots.
The research of knots first grew out of physics however has change into a central space of topology. They’re important to how scientists perceive 3D and 4D areas and have a pleasant and refined construction that researchers are nonetheless attempting to know.
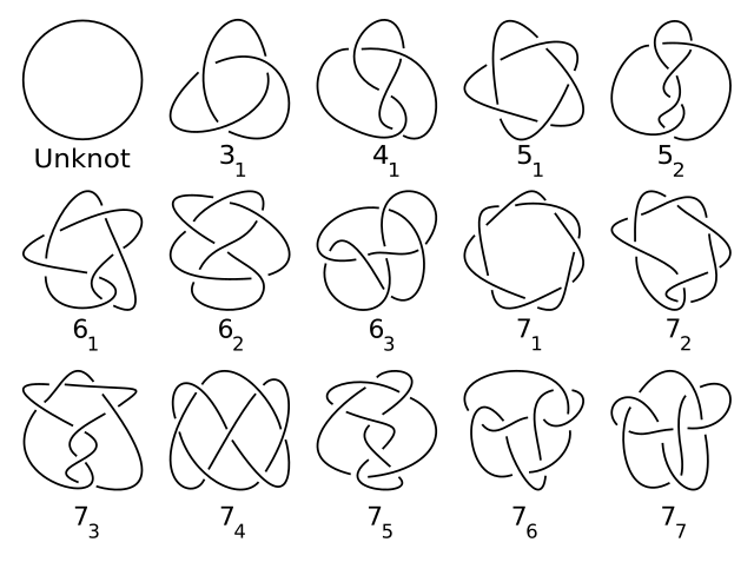
Knots are examples of areas that sit inside different areas.
Jkasd/Wikimedia Commons
As well as, knots have many functions, starting from string idea in physics to DNA recombination in biology to chirality in chemistry.
What form do you reside on?
Geometric topology is a phenomenal and sophisticated topic, and there are nonetheless numerous thrilling inquiries to reply about areas.
For instance, the graceful 4D Poincaré conjecture asks what the “simplest” closed 4D house is, and the slice-ribbon conjecture goals to know how knots in 3D areas relate to surfaces in 4D areas.
Topology is presently helpful in science and engineering. Unraveling extra mysteries of areas in all dimensions might be invaluable to understanding the world during which we stay and fixing real-world issues.



