Do artists and scientists see the identical factor within the form of bushes? As a scientist who research branching patterns in dwelling issues, I’m beginning to suppose so.
‘Tableau I’ by Piet Mondrian, 1921.
Kunstmuseum Den Haag
Piet Mondrian was an early Twentieth-century summary artist and artwork theorist obsessive about simplicity and essence of kind. Even individuals who have by no means heard of Mondrian will probably acknowledge his iconic irregular grids of rectangles.
After I noticed Mondrian’s 1911 “Gray Tree,” I instantly acknowledged one thing about bushes that I had struggled to explain. By eradicating all however essentially the most important components in an summary portray, Mondrian demonstrated one thing I used to be making an attempt to clarify utilizing physics and fractal geometry.

Gray Tree by Piet Mondrian, 1911.
Kunstmuseum Den Haag
My discipline of analysis is mathematical biology. My colleagues and I attempt to clarify how treelike buildings similar to veins and arteries, lungs and leaves fine-tune their bodily kind to effectively ship blood, air, water and vitamins.
Elementary analysis within the biology of branching helps treatment cardiovascular illnesses and most cancers, design supplies that may heal themselves and predict how bushes will reply to a altering local weather. Branching additionally exhibits up in ant foraging patterns, slime molds and cities.
The treeless tree

‘Polder Landscape with Silhouetted Young Tree’ by Piet Mondrian, 1900-1901.
Wikimedia Commons
From 1890 to 1912, Mondrian painted dozens of bushes. He began with full-color, lifelike bushes in context: bushes in a farmyard or a dappled lane. Step by step he eliminated leaves, depth, coloration and finally even branching from his tree work. “Gray Tree” makes use of solely curved traces of varied thickness superimposed on high of each other at seemingly random angles. But the picture is unmistakably a tree.
How did Mondrian convey the sense of a tree with so little? The science of bushes could provide some clues.
The science of branching
One purpose of mathematical biology is to synthesize what scientists know concerning the huge variety of dwelling methods – the place there appears to be an exception to each rule – into clear, normal ideas, ideally with few exceptions. One such normal precept is that evolution fine-tunes treelike buildings in dwelling issues to make metabolism and respiration as environment friendly as doable.
The physique rigorously controls the thickness of vessels as they department, as a result of deviation from essentially the most environment friendly diameter wastes power and causes illness, similar to atherosclerosis.
In lots of circumstances, similar to human blood vessels, the physique exerts a lot tighter management over diameter than size. So whereas veins and arteries would possibly take circuitous routes to accommodate the vagaries of organs and anatomy, their diameter normally stays inside 10% of the optimum. The identical precept seems in tree branches as properly.
The exact calibration of department diameter results in an indicator of fractal shapes referred to as scale invariance. A scale invariance is a property that holds true whatever the dimension of an object or a part of an object you’re . Scale invariance happens in bushes as a result of trunks, limbs and twigs all department in related methods and for related causes.
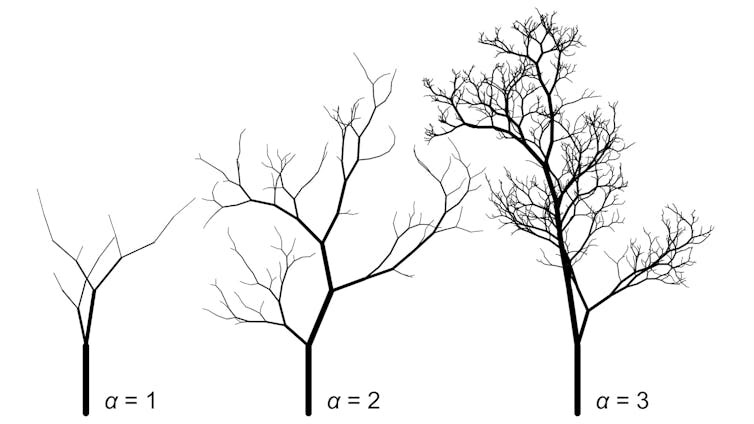
Timber with totally different values of the scaling parameter α.
Gao and Newberry/PNAS Nexus
The size invariance in department diameter dictates how a lot smaller a limb ought to be because it branches and the way a lot funding a tree makes in a couple of thick branches versus many skinny ones. Timber have advanced scale invariance to move water, attain gentle and resist gravity and wind load as effectively as doable given bodily limits.
This science of bushes impressed my colleague and me to measure the scaling of tree department diameter in artwork.
The artwork of bushes
Amongst my favourite photos is a carving of a tree from a late-medieval mosque in India. Its exaltation of bushes jogs my memory of Tolkien’s Tree of Gondor and the human capability to understand the easy great thing about dwelling issues.

Siddi Saiyyed Mosque in Ahmedabad, Gujarat, India, c. 1572.
SHIVREKHA/Wikimedia Commons
However I additionally discover mathematical inspiration within the Islamic Golden Age, a time when artwork, structure, math and physics thrived. Medieval Islamic architects even embellished buildings with infinitely nonrepeating tiling patterns that weren’t understood by Western arithmetic till the Twentieth century.

‘Cherry Blossoms’ by Matsumura Goshun (1752–1811).
Metropolitan Museum of Artwork
The stylized tree carvings of the Sidi Saiyyed mosque additionally observe the exact system of proportions dictated by the size invariance of actual bushes. This degree of precision of department diameter takes an attentive eye and a cautious plan – significantly better than I may freehand.
Certainly, wherever our group checked out bushes in nice art work, similar to Klimt’s “Tree of Life” or Matsumura Goshun’s “Cherry Blossoms,” we additionally discovered exact scale invariance within the diameter of branches.
“Grey Tree” additionally realistically captures the pure variation in department diameters, even when the portray offers the viewer little else to go on. With out lifelike scaling, would this portray even be a tree?
As if to show the purpose, Mondrian made a subsequent portray the next yr, additionally with a grey background, curved traces and the identical general composition and dimensions. Even the place of a number of the traces are the identical.
However, in “Blooming Apple Tree” (1912), all of the traces are the identical thickness. The scaling is gone, and with it, the tree. Earlier than studying the title, most viewers wouldn’t guess that this can be a portray of a tree. But Mondrian’s sketches reveal that “Blooming Apple Tree” and “Gray Tree” are the exact same tree.

‘Blooming Apple Tree’ by Piet Mondrian, 1912.
Kunstmuseum Den Haag
The 2 work include few components which may sign a tree – a focus of traces close to the middle, traces that could possibly be branches or a central trunk and features that would point out the bottom or a horizon.
But solely “Gray Tree” has scale-invariant department diameters. When Mondrian removes the size invariance in “Blooming Apple Tree,” viewers simply as simply see fish, scales, dancers, water or just nonrepresentational shapes, whereas the tree in “Gray Tree” is unmistakable.
Photograph synthesis
Mondrian’s tree work and scientific idea spotlight the significance of the thickness of tree branches. Consilience is when totally different traces of proof and reasoning attain the identical conclusions. Artwork and math each discover summary descriptions of the world, and so seeing nice artwork and science pick the identical important options of bushes is satisfying past what artwork or science may accomplish alone.
Simply as nice literature similar to “The Overstory” and “The Botany of Desire” present us how bushes affect our lives in methods we regularly don’t discover, the artwork and science of bushes present how people are finely attuned to what’s vital to bushes. I feel this resonance is one purpose folks discover fractals and pure landscapes so pleasing and reassuring.
All these traces of pondering give us new methods to understand bushes.



